
Si l’on doit bien à Albert Einstein (1879 – 1955) la théorie de relativité restreinte1Albert Einstein, 1905. « Zur Elektrodynamik bewegter Körper », Annalen der Physik, n° 17, pp. 891 – 921. Consultable en ligne. Version française disponible en ligne. ainsi que celle de la relativité générale2Albert Einstein, 1916. « Die Grundlage der allgemeinen Relativitätstheorie », Annalen der Physik, n° 49, pp. 769 – 822. Consultable en ligne. Maurice Solovine en a réalisé une traduction française dans : Albert Einstein, 1933. Les Fondements de la théorie de la relativité générale, suivi de : Théorie unitaire de la gravitation et de l’électricité, suivi de : Sur la Structure cosmologique de l’espace, Hermann et compagnie., le principe de relativité a été introduit en physique bien avant. On parle de relativité galiléenne et son instigateur est… Giordano Bruno (1548 – 1600). Il y avait un piège !
Bien entendu, si l’on qualifie cette première forme de relativité physique de « galiléenne », c’est bien parce que Galilée a joué quelque rôle dans sa formulation. L’introduction de ce principe est un des principaux éléments de la révolution épistémologique à laquelle j’avais fait allusion précédemment. Le présent article se place donc dans la suite de la série sur l’histoire des sciences que j’ai entamée. Il me permettra également, une fois de plus, d’introduire quelques notions qui seront utiles pour les futurs articles de vulgarisations à venir.
Ça s’en va et ça revient !
L’introduction du principe de relativité est liée à l’introduction de l’héliocentrisme, c’est-à-dire à la prise de conscience que non seulement la Terre n’est pas au centre du Monde, mais également qu’elle tourne sur elle-même et autour du Soleil.
Les observations des planètes avaient mis au jour des anomalies dans leurs orbites. Ainsi, elles semblent parfois rebrousser chemin, avant de repartir en avant :
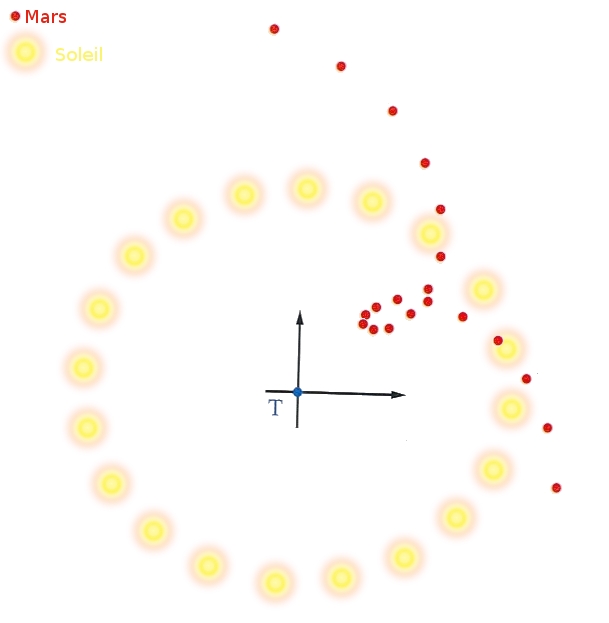
Pour résoudre les problèmes des modèles de l’époque, Nicolas Copernic (1473 – 1543) indiqua que le plus simple pour expliquer les observations serait que la Terre ne soit pas immobile, mais qu’elle tournât sur elle-même et autour du Soleil3Nicolaus Copernicus, 1543. De revolutionibus orbium cœlestium, Johann Petreium. Disponible en ligne. Une traduction française par Alexandre Koyré peut être trouvé dans : Nicolas Copernic, 1998. Des Révolutions des orbes célestes, Pergame.. Pour mieux dire, cela correspondait mieux au principe de parcimonie, c’est-à-dire que cette explication nécessitait moins d’hypothèses que les autres modèles – je traite du principe de parcimonie dans un autre article et je vous invite également à voir ce qu’en dit Jean-Pierre Luminet. Non seulement ce modèle était-il plus parcimonieux, mais également permettait-il d’expliquer toutes les observations, ce qui n’était pas le cas des modèles précédents.

Avant Nicolas Copernic, Nicole Oresme (vers 1320 ou 1322 – 1382) avait déjà présenté le système héliocentrique comme crédible4Nicole Oresme, 1377. Livre du Ciel et du monde.. Cependant, Nicolas Copernic apporte en plus la démonstration mathématique, c’est-à-dire géométrique, de sa validité. Ce sera un autre point important de la révolution qui s’annonce.
Aristote et Giordano Bruno sont sur un bateau
Toutefois, des modèles dans lesquels la Terre n’était pas au centre du Monde avaient été proposés dès l’Antiquité, tel celui d’Aristarque de Samos (vers 310 – 230 avant J.-C.), que l’on connait surtout par l’intermédiaire de la présentation qu’en fit Archimède (vers 287 – 212 avant J.-C.)5Αρχιμήδης, Ψαµµίτης. Disponible en ligne. Une version française est disponible en ligne également.. Il est également probable que la théorie héliocentrique était apparue en Inde bien avant encore – le propos de cet article étant de parler de l’introduction du principe de relativité en physique et non pas de l’histoire des systèmes cosmogoniques, je ne la détaillerais pas plus avant dans l’immédiat, mais faite moi savoir dans les commentaires si vous êtes intéressé pour que je fasse un article sur ce sujet. De même, l’idée que l’on puisse expliquer le Monde par les mathématiques remonte probablement à Pythagore (vers 580 – vers 495 avant J.-C.).
Cependant, ces systèmes avaient été abandonnés et peu à peu oubliés du fait de la prééminence du système philosophique (terme qui regroupait à l’époque l’ensemble des champs du savoir) d’Aristote (384 – 322 avant J.-C.). Ce système est souvent présenté de manière un peu caricaturale, ce qui fait que l’on a parfois un peu de mal à comprendre les raisons pour lesquelles son influence a été aussi grande. Je vais essayer de ne pas tomber dans cet écueil.

Aristote avait fondé une école, le Lycée. Au sein de cette école, il prétendait enseigner tous les savoirs de l’époque, de sorte qu’il s’est attelé à produire un système dont l’ambition était de pouvoir expliquer l’intégralité du Monde. Il a réalisé cette tâche selon un système logique qu’il avait établi, la logique aristotélicienne. Il en a résulté un système extrêmement cohérent et complet. Une autre conséquence est que remettre en cause un élément de ce système revient très vite à remettre en cause l’intégralité du système, de sorte que l’on n’a guère plus que deux alternatives à son égard : soit on adhère à l’intégralité du système aristotélicien, soit on le rejette entièrement. Justement, il était possible de rendre ce système compatible avec la Bible, ce qui fait qu’armé de la Bible et du système aristotélicien, on était pendant longtemps intégralement capable d’expliquer le Monde. À quelques problèmes près… Comme remettre en cause un seul élément provoquait la remise en cause de l’ensemble du système, pendant longtemps ces problèmes étaient généralement considérés comme des artefacts qui ne méritaient pas que l’on s’attardât dessus.

Selon Aristote, le Cosmos, délimité par le cercle extérieur où sont situés les étoiles et au milieu duquel siège – immobile – la Terre, est divisé en deux zones. La première est le monde sublunaire (au-dessous de la Lune), domaine de quatre éléments – terre, air, eau, feux – et sujet au changement, qui est le monde où nous vivons. La deuxième zone, où se trouvent le soleil, les planètes et les étoiles, est le monde supralunaire (au-delà de la Lune), domaine du cinquième élément (la quintessence) et de la perfection. Ces deux mondes ne répondent pas aux mêmes règles. Dans le monde supralunaire, tout n’est que perfection, cercles et sphères. Dans le monde sublunaire, le mouvement naturel est rectiligne, l’air et le feu allant vers le haut, tandis que l’eau et la terre vont vers le bas6Ἀριστοτέλης. Περὶ οὐρανοῦ. Consultable en ligne. Une version française : Aristote, 2003. Du Ciel, Les Belles Lettres. Consultable en ligne.. Le géocentrisme de Claude Ptolémée (90 après J.-C. – 168) est compatible avec le système aristotélicien7Κλαύδιος Πτολεμαῖος, environ 150 après J.-C. Μαθηματική σύνταξις. Une version française par Nicolas Halma : Claude Ptolémée, 1927. Almageste, Hermann. Les deux tomes sont consultables en ligne.. Selon Aristote, la Terre ne peut pas être en rotation, car sinon les mouvements rectilignes seraient altérés, de sorte que si l’on laissait tomber un objet d’une hauteur, par exemple d’une tour, alors il ne tomberait pas au pied de la tour. Comme l’on observe que les objets lancés depuis une tour arrive à son pied, dans le système aristotélicien c’est la preuve que la Terre n’est pas en rotation.
Giordano Bruno va contredire cet argument8Giordano Bruno, 1584. La cena de le Ceneri, John Charlewood.. En effet, il fît remarquer que si l’on se place sur un navire se déplaçant en ligne droite et sans changer de vitesse (on parle désormais de mouvement rectiligne uniforme), alors un objet lâché du sommet d’un mât du bateau atterri au pied de ce mât.
Comme il était difficile de réaliser une vidéo lisible en faisant l’expérience sur un bateau, je suis monté sur un chariot. Cependant, le résultat est le même. Si le chariot est immobile, un objet lâché sans vitesse initiale tombe à mes pieds :
Vous aurez sans doute constaté que le film est ralenti, à 60 % de sa vitesse initiale (et également fortement recadré). La raison en est qu’à vitesse normale, c’est trop court, on ne voit presque rien.
Si maintenant le chariot se déplace à une vitesse rectiligne et uniforme, l’objet tombe toujours à mes pieds :
En conséquence, le fait que la chute des objets ait lieue selon une ligne droite ne peut pas être considéré comme une preuve de l’immobilité de la Terre.
Cela signifie également que l’observation n’est pas la même en fonction du point de vue dans lequel on se place : pour un individu situé sur le bateau (ou bien sur le chariot dans mon cas), l’objet suit une trajectoire rectiligne verticale qui va du haut vers le bas. Pour un observateur sur la rive (pour un observateur à côté de ma caméra), l’objet décrit une trajectoire certes rectiligne, mais cette fois-ci oblique, à la fois du haut vers le bas, mais également dans le sens de déplacement du navire (du chariot). Le mouvement est donc relatif au point de vue dans lequel on se place (on parle désormais de référentiel).
Giordano Bruno ne formalisera pas plus avant ce principe de relativité. Il n’en eut guère le temps. En effet, non content de soutenir le système copernicien, donc de contredire Aristote, ce que l’on aurait éventuellement pût lui passer même à l’époque, il défendait également toute une série d’opinions que l’Église considérait comme inacceptables. Ainsi, il soutenait que l’Univers était infini et peuplé de mondes comparables au nôtre. Également, il était panthéiste, c’est-à-dire qu’il considérait que Dieu n’était pas unique, mais s’incarnait dans tout. Ce n’est pas fini, car il proclamait que Jésus-Christ n’était pas Dieu, mais un simple « mage habile », que le Saint-Esprit était l’âme du Monde, que Satan serait finalement sauvé et encore d’autres audaces. Il fût donc arrêté par l’Inquisition en 1592 et brulé en 1600. Cependant, ses écrits attirèrent notamment l’attention d’un certain Galileo Galilei – francisé en Galilée – (1564 – 1642)…
Galilée regarde par le bon bout de la lorgnette

Dans une lettre adressée à Johannes Kepler (1571 – 1630) en 1597 (ce dernier était lui-même convaincu de la validité du modèle copernicien), Galilée affirme souscrire à la validité des théories copernicienne depuis plusieurs années9Jean-Pierre Maury, 1986. Galilée, le messager des étoiles, Découvertes Gallimard sciences.. Il y déclare également n’avoir alors rien osé publier. Pour pouvoir se lancer dans la défense du modèle de Nicolas Copernic, il lui faut d’abord s’assurer qu’il sera bien en mesure d’apporter des preuves solides.
En 1609, un ancien de ses élèves lui fait part de l’invention du hollandais Hans Lippershey (1570 – 1619) : la lunette. Beaucoup d’universitaires de l’époque la considère comme un jouet, mais Galilée n’est pas de cet avis. Il en fabrique plusieurs, dans l’objectif de réaliser des observations astronomiques.
Le premier astre que Galilée va observer sera la Lune. Il va rapidement constater qu’elle n’est pas lisse et parfaite, polie comme du cristal, comme le prétend le modèle aristotélicien. Au contraire, elle est montagneuse. Voilà la preuve qu’il cherchait de l’invalidité du système aristotélicien10Galileus Galileus, 1610. Sidereus nuncius, Thomam Baglionum. Téléchargeable en ligne. Une traduction française de Fernand Hallyn : Galilée, 1992. Le Messager des étoiles, Seuil. Consultable en ligne.. Plus encore, si la Lune est montagneuse, alors elle n’est pas si différente de la Terre, on peut donc partir du principe, contrairement à ce qu’affirmait Aristote, que les lois physiques sont les mêmes sur Terre et dans le reste du Cosmos. Avec ces deux postulats, Galilée fonde la science moderne : les lois de la physique sont universelles et les mathématiques forment le langage adéquat pour les formuler11Galileo Galilei, 1623. Il Saggiatore. Une traduction française : Christiane Chauviré, 1980. L’Essayeur de Galilée, Annales littéraires de l’université de Besançon, Les Belles lettres, Paris..
Les travaux de Galilée feront l’objet de plusieurs contestations. Parmi elles, assez légitimement, on lui fit remarquer que le principe de fonctionnement de la lunette n’était pas connu, de sorte que l’on ne pouvait pas être certain que ce que l’on observait en l’utilisant n’était pas une illusion. Johannes Kepler réalisera une étude physique et mathématique de la lunette, ce qui coupera court à cet argument12Johannes Kepler, 1611. Dioptricae..
Encore une fois, le propos du présent article n’est pas l’histoire de la cosmologie, pour passionnante qu’elle soit. Résumons donc les deux décennies suivantes en disant que les réfutations des travaux de Galilée furent nombreuses, auxquelles ce dernier opposa à chaque fois des arguments scientifiques très forts. De sorte que, sur le terrain scientifique, il apparaissait clairement comme le triomphateur. Cela lui apportera des inimitiés avant tout politiques, mais très fortes elles aussi. En effet, sa remise en cause intégrale du système aristotélicien mettait à mal la position d’universitaires qui avaient bâties toutes leurs carrières sur ce système. Ne pouvant pas l’attaquer sur le plan scientifique, les adversaires de Galilée vont faire en sorte que la controverse devienne religieuse.
En 1624, le pape Urbain VIII (1568 – 1644) commande à Galilée un ouvrage présentant de manière neutre le système de Ptolémée et celui de Copernic. C’est ainsi qu’en 1632 est publié le Dialogue sur les deux grands systèmes du monde13Galileo Galilei, 1632. Dialogo sopra i due massimi sistemi del mondo, Batista Landini. Consultable en ligne. Une traduction française de René Fréreux et François de Gandt : Galilée, 2000. Dialogue sur les deux grands systèmes du monde, Seuil, Points Sciences. (que j’ai déjà mentionné dans un article précédent). Dans cet ouvrage, le modèle copernicien sort clairement renforcé par rapport au modèle de Ptolémée. C’est aussi dans cet ouvrage que Galilée répond de nouveau à l’argument de la chute rectiligne des corps comme réfutation de la mobilité de la Terre. À cette occasion, il formalise le principe de relativité :
« Enfermez-vous avec un ami dans la cabine principale à l’intérieur d’un grand bateau et prenez avec vous des mouches, des papillons, et d’autres petits animaux volants. Prenez une grande cuve d’eau avec un poisson dedans, suspendez une bouteille qui se vide goutte à goutte dans un grand récipient en dessous d’elle. Avec le bateau à l’arrêt, observez soigneusement comment les petits animaux volent à des vitesses égales vers tous les côtés de la cabine. Le poisson nage indifféremment dans toutes les directions, les gouttes tombent dans le récipient en dessous, et si vous lancez quelque chose à votre ami, vous n’avez pas besoin de le lancer plus fort dans une direction que dans une autre, les distances étant égales, et si vous sautez à pieds joints, vous franchissez des distances égales dans toutes les directions. Lorsque vous aurez observé toutes ces choses soigneusement (bien qu’il n’y ait aucun doute que lorsque le bateau est à l’arrêt, les choses doivent se passer ainsi), faites avancer le bateau à l’allure qui vous plaira, pour autant que la vitesse soit uniforme [c’est-à-dire constante] et ne fluctue pas de part et d’autre. Vous ne verrez pas le moindre changement dans aucun des effets mentionnés et même aucun d’eux ne vous permettra de dire si le bateau est en mouvement ou à l’arrêt. »
Cela signifie que l’on ne peut pas distinguer l’immobilité d’un mouvement rectiligne uniforme sans avoir un point de repère extérieur. Autrement dit, un mouvement rectiligne uniforme ne peut être observé que par rapport à une référence. Le mouvement est donc une notion relative : être immobile est équivalent à être en mouvement rectiligne uniforme. Plus encore, il n’y a pas de point de vue privilégié, pas de position absolue, tous les points de vue (tous les référentiels) sont aussi valides les uns que les autres – à l’aide des transformations (opérations mathématiques) galiléennes, on peut passer d’un point de vue à un autre, c’est-à-dire changer de référentiel.
Ainsi, tandis que Giordano Bruno mettait en évidence le fait que la chute rectiligne des objets n’est pas une preuve de l’immobilité de la Terre, Galilée pour sa part montrait qu’on aura beau multiplier les observations, le seul moyen de déterminer si l’on se trouve en mouvement (rectiligne uniforme), c’est d’utiliser une référence extérieure.
On peut visualiser la relativité galiléenne dans le jeu vidéo Super Mario Bros.14Shigeru Miyamoto et Takashi Tezuka, 1985. Super Mario Bros., Nintendo.. En effet, dans ce jeu, lorsque Mario atteint le centre de l’écran, son sprite n’avance plus dans l’écran, c’est le sol qui se déplace sous ses pas. On a adopté un point de vue centré sur Mario, de sorte que le monde semble se déplacer plutôt que Mario :
J’ai trouvé cette idée de prendre Super Mario Bros. comme exemple de la relativité galiléenne chez e-Penser.
Galilée sera finalement condamné par l’Inquisition en 1633 à abjurer ses théories, mais au moins n’est-il mis à mort. Il parviendra néanmoins à faire publier un dernier ouvrage, en 1638, le Discours sur deux sciences nouvelles15Galileo Galilei, 1638. Discorsi e Dimonstrazioni matematiche intorno a due scienze attenanti alla mecanica ed i movimenti locali, Louis Elzevier. Disponible en ligne. Une version française : Galilée, 1995. Discours concernant deux sciences nouvelles, Presses Universitaires de France.. Au cours de sa carrière, il a également réalisé des contributions importantes concernant la chute des corps et la mécanique des fluides dont il sera prochainement question, vu d’ici.
Une part d’absolu
Si véritablement tout était relatif, alors cette phrase le serait également et serait donc fausse…
Je dois cette judicieuse remarque à Étienne Klein.
Ainsi, contrairement à ce que sous-entend le titre de cet article, variation sur une affirmation que l’on entend couramment, la relativité galiléenne, pas plus que la relativité restreinte ou la relativité générale, ne prétend pas que tout soit relatif. La relativité galiléenne indique que le mouvement est relatif au point de vue depuis lequel on l’observe. En revanche, le temps y est absolu : deux événements vus simultanément depuis un référentiel seront perçus comme simultanés dans tout autre référentiel, c’est-à-dire que dans une chronologie donnée, un évènement donné à lieu à la même date quel que soit le référentiel. Également, les principes physiques s’appliquent de la même façon lorsque l’on est immobile ou lorsque l’on est en mouvement rectiligne uniforme – ce dernier point est désormais appelé le principe d’inertie, formalisé par Isaac Newton (1643 – 1727), sujet dont je traiterais prochainement.
Dans le cadre de la relativité restreinte, ainsi que de la relativité générale (qui est une généralisation de la relativité restreinte à la gravitation), le mouvement est toujours relatif, mais également le temps : la simultanéité n’est pas conservée par changement de référentiel, autrement dit la date où a lieu un évènement dépend du référentiel. À l’inverse, il existe une vitesse limite, la vitesse de la lumière, qui est absolue quel que soit le référentiel. De plus, la relativité générale indique que les effets de la gravitation sont équivalents aux effets d’une accélération et que ceci est vrai quelle que soit la localisation dans l’espace-temps (ce que l’on nomme principe d’équivalence). La relativité introduite par Albert Einstein pousse donc plus loin encore le principe de relativité. Cependant, elle indique elle aussi que certaines choses sont absolues. J’ai également prévu de traiter des relativités restreinte et générale dans ce journal.
Une histoire qui continue
Cet article m’a permis d’introduire le principe de relativité galiléenne, mais aussi d’aborder la notion de référentiel, dont nous reparlerons, notamment lorsqu’il sera question d’Isaac Newton. Il m’a également permis d’indiquer deux principes fondamentaux de la science moderne. D’une part, l’universalité des lois de la physique, c’est-à-dire le principe selon lequel la physique s’applique de la même façon en tout point de l’Univers. D’autre part, le principe selon lequel les mathématiques sont le bon formalisme pour la physique. Ces deux principes sont à l’origine de l’extrême fécondité de la physique depuis la révolution copernicienne.
Par ailleurs, cette histoire m’a permis de mettre en lumière deux points qui me semblent importants.
Le premier est que le travail de recherche n’est pas le fait d’un individu isolé. Certes, à l’époque de Galilée les publications des chercheurs n’ont qu’un seul auteur, mais, par exemple, la formalisation de l’héliocentrisme est un travail réalisé par au moins trois personnes différentes : Nicolas Copernic a théorisé un modèle, Galilée a réalisé les observations validant ce modèle et Johannes Kepler a produit le formalisme permettant de justifier de la validité des observations. De même, le principe de relativité galiléenne a été introduit par Giordano Bruno et formalisé par Galilée. Si l’on peut trouver dans l’histoire des sciences quelques cas, de fait célèbres, de contributions majeures dues à une seule personne isolée, la majorité des avancées importantes impliquent plusieurs chercheurs.
Le deuxième point tient au statut du système aristotélicien. S’il a pendant longtemps pu être considéré comme insurpassable, il est désormais souvent vu, un peu caricaturalement, comme un exemple de complet fourvoiement, l’archétype de l’erreur. Une des raisons de cet état de fait est sans doute la difficulté de remonter aux textes initiaux. Cependant, je pense qu’il y a également des causes plus profondes.
Tout d’abord, il me semble qu’une vision assez linéaire de l’Histoire est répandue. Dans cette vision, le Moyen-âge (environ 1 000 ans tout de même) est vu comme une sombre période de stagnation, voire de régression. En ce sens, le système aristotélicien est vu comme un carcan qu’il a fallu briser pour retrouver la voie du progrès. Cependant, il me semble que les choses sont sensiblement plus complexes.
Ensuite, on a souvent une vision très aristocratique de la science : quelques individus supérieurs toucheraient une vérité que les autres n’ont pas su déceler. Je pense que c’est non seulement un mauvais point de vu, mais même dangereux.
Je l’ai déjà indiqué, la science, ce n’est pas tant le doute que la recherche de l’erreur. Tout le long de cet article, j’ai, volontairement, régulièrement utilisé le terme moderne de « modèle », tandis qu’à l’époque on parlait plutôt de « système » : il y avait un propos caché – oui, je suis manipulateur !
Confronté à un phénomène donné, on cherche les éléments qui permettent de l’expliquer, en tentant de prendre en compte tout ce qui a une influence sur ce phénomène et rien d’autre. C’est ce que l’on appelle un modèle. On cherche alors les erreurs dans ce modèle, par exemple à l’aide d’observations. Une fois le modèle validé, il permet de faire des prévisions et de comprendre certains mécanismes profonds du phénomène, jusqu’à ce qu’on atteigne les limites du modèle et qu’on en propose un nouveau. Dans un tel cadre, les erreurs d’un modèle sont riches d’enseignements et présentent un réel intérêt.
En cela, le système aristotélicien, en tant que système ambitionnant d’expliquer intégralement le Monde en un ensemble intrinsèquement cohérent et en tant que synthèse de l’essentiel des savoirs de son époque, était une contribution importante. S’il est désormais intégralement réfuté, ses erreurs n’en ont pas moins été extrêmement fécondes. Les grands noms de la science, sans minimiser l’importance de leurs contributions, on tous eut tort à un moment donné, ou bien n’ont eu que des explications partielles : une grande partie du travail scientifique consiste à se tromper ! Puis à rechercher les erreurs…
Le problème avec le système aristotélicien n’était donc certainement pas le système lui-même, mais ce que l’on en a fait. À savoir, précisément, que l’on a eut ce point de vue aristocratique considérant qu’il y avait des individus à l’entendement dépassant celui de la masse, dont la pensée serait donc intrinsèquement supérieure à celle que quiconque pourrait produire. De sorte qu’au lieu de chercher les erreurs du système, donc de faire de la science, on s’est contenté de paraphraser ce système, c’est-à-dire de faire du dogmatisme.
Il serait dommage de continuer à faire de même de nos jours, fusse dans le sens inverse…
Notes
| ↑1 | Albert Einstein, 1905. « Zur Elektrodynamik bewegter Körper », Annalen der Physik, n° 17, pp. 891 – 921. Consultable en ligne. Version française disponible en ligne. |
|---|---|
| ↑2 | Albert Einstein, 1916. « Die Grundlage der allgemeinen Relativitätstheorie », Annalen der Physik, n° 49, pp. 769 – 822. Consultable en ligne. Maurice Solovine en a réalisé une traduction française dans : Albert Einstein, 1933. Les Fondements de la théorie de la relativité générale, suivi de : Théorie unitaire de la gravitation et de l’électricité, suivi de : Sur la Structure cosmologique de l’espace, Hermann et compagnie. |
| ↑3 | Nicolaus Copernicus, 1543. De revolutionibus orbium cœlestium, Johann Petreium. Disponible en ligne. Une traduction française par Alexandre Koyré peut être trouvé dans : Nicolas Copernic, 1998. Des Révolutions des orbes célestes, Pergame. |
| ↑4 | Nicole Oresme, 1377. Livre du Ciel et du monde. |
| ↑5 | Αρχιμήδης, Ψαµµίτης. Disponible en ligne. Une version française est disponible en ligne également. |
| ↑6 | Ἀριστοτέλης. Περὶ οὐρανοῦ. Consultable en ligne. Une version française : Aristote, 2003. Du Ciel, Les Belles Lettres. Consultable en ligne. |
| ↑7 | Κλαύδιος Πτολεμαῖος, environ 150 après J.-C. Μαθηματική σύνταξις. Une version française par Nicolas Halma : Claude Ptolémée, 1927. Almageste, Hermann. Les deux tomes sont consultables en ligne. |
| ↑8 | Giordano Bruno, 1584. La cena de le Ceneri, John Charlewood. |
| ↑9 | Jean-Pierre Maury, 1986. Galilée, le messager des étoiles, Découvertes Gallimard sciences. |
| ↑10 | Galileus Galileus, 1610. Sidereus nuncius, Thomam Baglionum. Téléchargeable en ligne. Une traduction française de Fernand Hallyn : Galilée, 1992. Le Messager des étoiles, Seuil. Consultable en ligne. |
| ↑11 | Galileo Galilei, 1623. Il Saggiatore. Une traduction française : Christiane Chauviré, 1980. L’Essayeur de Galilée, Annales littéraires de l’université de Besançon, Les Belles lettres, Paris. |
| ↑12 | Johannes Kepler, 1611. Dioptricae. |
| ↑13 | Galileo Galilei, 1632. Dialogo sopra i due massimi sistemi del mondo, Batista Landini. Consultable en ligne. Une traduction française de René Fréreux et François de Gandt : Galilée, 2000. Dialogue sur les deux grands systèmes du monde, Seuil, Points Sciences. |
| ↑14 | Shigeru Miyamoto et Takashi Tezuka, 1985. Super Mario Bros., Nintendo. |
| ↑15 | Galileo Galilei, 1638. Discorsi e Dimonstrazioni matematiche intorno a due scienze attenanti alla mecanica ed i movimenti locali, Louis Elzevier. Disponible en ligne. Une version française : Galilée, 1995. Discours concernant deux sciences nouvelles, Presses Universitaires de France. |
Je me lève et j'applaudis à 10 mains pour l'utilisation, pertinente et en plus tout à fait à propos dans ce contexte de 30e anniversaire, de Super Mario Bros !
Par ailleurs, je serais tout à fait intéressé par une "histoire" des système cosmogoniques.
En effet, l’utilisation de Mario tombe bien, vu la date. Cela dit, il faut rendre à Bruce Benamran ce qui lui revient : c’est en regardant une de ses vidéos que j’ai eu l’idée d’utiliser le plombier moustachu. S’il ne l’avait pas fait avant moi, je ne sais pas si j’aurais eu l’idée. Imaginez : j’aurais peut-être même utilisé Sonic !
En tout cas, ça tombait particulièrement bien, parce que je n’étais vraiment pas certain que l’explication de la relativité galiléenne était probante. J’ai l’impression qu’en ajoutant Mario, les choses deviennent claires – s’il y a des éléments confus, il ne faut pas hésiter à me le faire remarquer.
Cela dit, en creux, l’article contient une critique du runing gag sur Aristote d’e-Penser. Ce n’était vraiment pas l’objectif, disons que c’est un dégât collatéral…
En tout cas, je prends bonne note de l’intérêt sur l’histoire des cosmogonies. J’ai suffisamment peu de lecteurs réguliers pour en prendre soin ! Ça va me demander de me plonger dans des textes védiques, je ne sais pas encore comment je vais faire, mais ça me sera formateur, au moins. De toute façon, je me rends compte qu’au vu de la tournure que prennent les articles, il sera nécessaire que j’aborde les révolutions du XXe siècle – la crise des fondements en mathématiques, les relativités restreinte et générale, ainsi que la mécanique quantique. Du coup, ça ouvrira la voie aux systèmes cosmogoniques.
Sinon, en passant, parlons de la vie du site : j’essaye de lui ajouter des outils facilitant le partage – si ce site n’est pas lu, ça n’a que peu d’intérêt – et permettant de mieux formater les commentaires. J’espère que ça facilitera la vie des lecteurs.
Mon Dieu, Sonic, mais vous n'y pensiez pas sérieusement, vous ne voudriez quand pas voir toute votre crédibilité scientifique acquise de haute lutte balayée pour une référence amusante mais non moins hasardeuse ? ^_^
Au pire, je pourrais toujours écrire un livre avec les frères Bogdanoff pour me refaire !
Honnêtement, je ne sais pas si je ne vais pas payer un jour ce commentaire, mais, un peu comme Cyrano, parfois je ne peux pas résister à un bon mot…
Vu qu'il y a un sondage toujours ouvert pour ajouter des personnages à Super Smash Bros sur Wii U, je pense suggérer à Nintendo d'y inclure ces chers frangins !